基本概念

树

基本概念

所有数据结构可以分为两种：线性结构和非线性结构。

  • 线性：列表，栈，队列，字符串等
  • 非线性：树，图

树中无环路。

节点的度数：指的是一个节点的子节点的数量

树的度数：树中所有节点的最大度数

叶节点：度数为零

层数：根节点的层数(level)为0。有些时候也规定为1。其他节点的层数=父节点层数+1

树深度：树中所有节点的最高层数

二叉树

每个节点都有两个子树（子树可以为空）。每个节点最多有两个子节点，而且有顺序，被称为左子节点和右子节点。

二叉树的性质

  • 如果共有n个节点，就有n-1条边
  • 第i层中最多有 2^i 个节点（规定根节点的层数为0）
  • 高度为h的二叉树最少有 h+1 个节点，而最多有 2^(h+1)-1 个节点
  • 如果叶节点的个数为 n0，度数为2的节点个数为 n2，那么 n0=n2+1

满二叉树和完全二叉树

如果高度为 h 的二叉树正好有 2^(h+1)-1 个节点，也就是所有节点完全填满，成为满二叉树。

完全二叉树中，所有节点按照先后次序排满底层再排高层，不会留下空隙。

对完全二叉树的所有节点从根开始从0标号，那么除了0号的根节点以外，第i号节点的父节点是⌊(i-1)/2⌋。同时，i号节点的左子节点是2*i+1，右子节点是2*i+2。如果是从1标号，那么更加好记，父节点是⌊i/2⌋，左子节点是i*2，右子节点是i*2+1

二叉树的表示

可以用数组表示：将每个节点在完全二叉树中的位置标号作为数组下标。

也可以用链表表示：每一个节点有本身的数据信息和左右子节点的引用。这样一来，树的数据结构中实际上只持有根节点的引用，其他节点都可以通过根找到。

或者用表格：每一行记录这个节点的数据，以及左右子节点对应行的索引。

二叉树的遍历

用V表示一个节点，L表示左子树，R表示右子树，四种遍历顺序是：

  • Preorder前序。VLR
  • Inorder中序。LVR
  • Postorder后序。LRV
  • Level order。按照层数先后访问

前三种遍历方法用递归可以很容易写出实现，而Level order可以使用队列实现。如果前三种方法不借助递归，则需要借助栈实现。

二叉树的应用

可以将任意一棵树通过左子女右兄弟表示法转化成二叉树。对于多棵树组成的森林也可以用这种方法把根视为兄弟连接起来，组成一棵二叉树。

一般的树遍历：

  • 深度优先遍历。又分为先序遍历和后序遍历。先序遍历先访问根，然后按照次序访问子树；后序遍历先访问所有子树，再访问根。如果对应到转化成的二叉树，则先序遍历和对应二叉树的先序遍历一致，后序遍历和对应二叉树的中序遍历一致。
  • 广度优先遍历。分层访问，按照层级进行访问。

线索树

如果用 节点的数据结构 表示树的话，会发现很多节点由于没有子树，其实含有不少空引用。如果能够利用这些指针帮助遍历，可以节约遍历的时间。在空引用中储存下一个遍历到的节点引用的二叉树，称为线索树。

在计算机内，通过增加标记来记录左右子树引用的位置究竟是真正的子女还是线索（遍历的前驱后继）。

常用的是中序线索树。构造中序线索树的时候，其实就是先对树进行一次中序遍历，用pre记录上一个节点，然后把pre的空引用利用起来。

霍夫曼树

每个节点带有权重，要使得节点的带权路径长度最小，需要构造一棵霍夫曼树。

Huffman 算法中，先将节点的权重从小到大排序，然后每次取出最小的两个节点，构造一个内节点作为两个节点的公共根，权重等于两个节点权重之和。然后把内节点放入序列中重新排序，再取两个最小的节点……如此反复直到只剩下一个节点，作为树的根。

如果内节点权重和外节点相等，则应该将内节点排在外节点后面，保证所有节点路径之和最小。

应用：霍夫曼编码：通过统计字符出现的频率，构造二进制编码使得电文长度最短。另外，为了译码，任意字符的编码不能是另一字符编码的前缀。就可以把频率作为权重，构造霍夫曼树。然后从根出发，左子树方向为0，右子树方向为1，写出每个字符的编码即可。

二叉搜索树

二叉搜索树中，严格按照每个节点的 左子节点>节点本身>右子节点 来排布，因此搜索树中的某个节点时不再需要遍历所有节点，而只需要一个O(log(n))复杂度的查找即可。

插入节点：通过递归算法插入节点，如果当前的节点比要插入的节点大，就插入到左子树中；如果当前节点比要插入的节点小，就插入到右子树中。终止条件是找到一个空子节点，然后将要插入的节点放在此处。

删除节点：使用递归方法，如果当前根节点是要删除的节点，就做删除操作；否则如果要删的节点比当前根节点小，就把左子树删掉目标节点，反之如果要删的节点比较大，就去右子树删除目标节点。找到节点位置删除时，如果是叶子节点，就把节点直接删除；如果该节点有一个子节点，就把子节点直接拼接到该节点的位置（删去一个竹节）；如果有左右两个节点，办法是从左子树中找到最大的节点（或者从右子树中找到最小的节点），把这个节点替换到当前的位置（这样就不会打乱搜索树的结构），之后从左子树（或右子树）中删掉选出的节点。

平衡的二叉搜索树

AVL树：Adelson-Velsky and Landis Tree

平衡二叉搜索树的特点是任意一个节点的左子树和右子树的高度相差不超过1.这样一来，树就不会因为插入顺序的缘故变得高度很高却不充实，影响查询效率。

为了保护平衡，需要在插入节点和删除节点对平衡做检查。为了方便实现，可以在树的节点数据结构中加一个当前节点高度的记录。

插入节点的操作：总体思路和二叉搜索树的插入接近，只不过每次递归拿到插入好的子树时，都需要对平衡进行检查，如果不满足平衡，需要进行一次平衡调整。平衡调整分为以下四种情况：

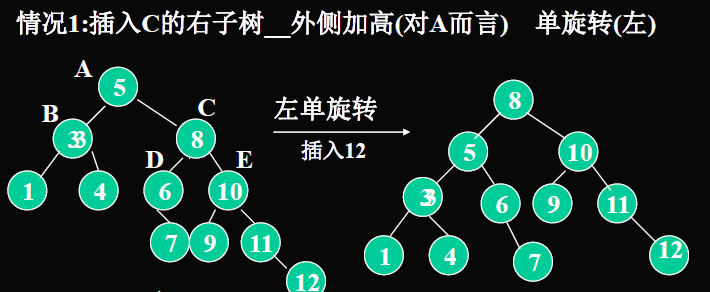
  • 右子树的右子树超高：进行一次左单旋转。将右子树的根节点提升为当前的根节点，然后原来的根节点和左子树部分整个作为左子树挂在新的根节点上。之前右子树的左子树挂在现在左子树的右子树上image-20210306150926962
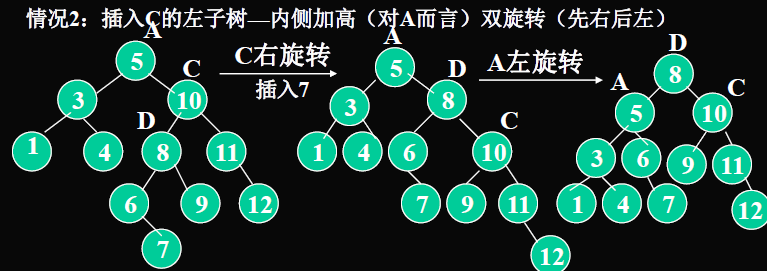
  • 右子树的左子树超高：先把右子树做一次右单旋转，就变化成了上面第一种情况。再进行一次左单旋转即可。image-20210306151219277
  • 左子树的左子树超高：进行一次右单旋转。
  • 左子树的右子树超高：左子树先进行一次左单旋转，变为上面一种情况。再进行一次右单旋转。

通过以上的平衡调整方法，在需要调整的节点调整前后，该节点位置的树高能保持和原来一致，因此变化不会波及到上层节点。也就是说，插入一个新节点最多进行一次调整即可再次平衡。

删除节点：和二叉搜索树的删除也是思路一样的。只不过删除之后要检查沿途每个节点的平衡情况。如果出现不平衡的情况，依然按照上面的平衡调整方法进行调整即可。但是删除节点时有可能造成不平衡的传递，也就是下层平衡调整后可能导致上层节点不平衡，因此每个沿途节点都要进行检查，而且可能进行不只一次的平衡调整。

斐波那契树：N层平衡二叉树至少有多少个节点？不妨这样思考：N层二叉树最坏的情况是一侧有N-1层，另一侧只有N-2层，而两侧又应该是节点最少的平衡二叉树。所以如果设最小的N层二叉树节点数是 Nh 那么 Nh = Nh-1 + Nh-2 +1。对比斐波那契数列就不难发现，其实形式是一样的。所以叫做斐波那契树。

B树

m路B树，指的是一个节点最多有m个子树的树。每个节点上，会在两个子树的引用直接夹杂一个元素，用来方便搜索，因此一个节点最多有m-1个这样的元素。

特点是，每个节点至少有一个元素，搜索时可以比较要搜的元素和该元素的大小关系：如果比这个元素小，那就去这个元素左边的子树上找；比这个元素大就去右边的元素找；也有可能要找的就是这个元素本身。

另外B树也要像平衡的二叉搜索树那样，要避免高度虚高。因此，对B树中除根节点以外每个节点做一个限制：最多有m个子节点，m-1个数据；最少有⌈m/2⌉个子节点，⌈m/2⌉-1个数据。此外，根节点至少有两个子节点，而且所有外节点（持有空子树的引用的节点）在同一层上。在进行插入和删除操作的时候就要考虑保持平衡。

插入节点时：如果能插在现有的叶节点上就直接插入。如果插入后超过了节点数限制，就把当前的节点分裂为两个子树和一个中间节点，中间节点转移到父节点上，并把两个子树接在父节点。但是中间节点的转移有可能使得父节点爆满，因此可能造成多次分裂，向上波及。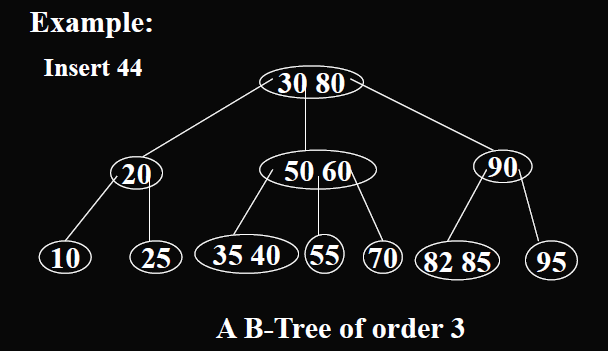image-20210306154805262 image-20210306154822466

删除节点：如果要删除的节点在叶节点上，直接删除。删除后有可能不满足平衡，就向邻居叶节点借一个元素。如果邻居也只有⌈m/2⌉-1个元素，就把两个节点合并。如果删除的节点不在叶节点上，则用左侧子树位于叶上最大的值（也可以是右侧子树上位于叶上最小的值）拿来和这个节点替换，然后转化成删除叶上节点的情况。

B+树：B树的变种：首先所有可能被索引到的节点（关键码）都出现在叶节点上，这意味着非叶节点上的数据只负责搜索。另外，叶节点上的关键码个数有另外的限制，并不一定和其他节点相同。叶节点上的指针用来指向对象，就可以进行对象的快速查找。每个叶节点多出的一个引用指向下一个兄弟叶节点，方便进行顺序搜索。B+树既可以从根节点向下随机搜索，又可以从指向最小关键码的叶节点指针开始进行顺序搜索。删除节点后上层索引中的关键码可以保留。